VINKEL MELLEM FLY

Lad os betragte to planer α 1 og α 2 givet henholdsvis af ligningerne:

Under vinkel mellem to planer mener vi en af ​​de dihedrale vinkler dannet af disse planer. Det er indlysende, at vinklen mellem normalvektorerne og planerne α 1 og α 2 er lig med en af ​​de angivne tilstødende dihedrale vinkler eller . Derfor . Fordi og , derefter

.

Eksempel. Bestem vinklen mellem planer x+2y-3z+4=0 og 2 x+3y+z+8=0.

Betingelse for parallelitet af to planer.

To planer α 1 og α 2 er parallelle, hvis og kun hvis deres normale vektorer og er parallelle, og derfor .

Så to planer er parallelle med hinanden, hvis og kun hvis koefficienterne ved de tilsvarende koordinater er proportionale:

eller

Betingelse for vinkelrethed af planer.

Det er klart, at to planer er vinkelrette, hvis og kun hvis deres normale vektorer er vinkelrette, og derfor eller .

På denne måde.

Eksempler.

DIREKTE I RUMMET.

VEKTORLIGNING DIREKTE.

PARAMETRISKE LIGNINGER DIREKTE

Positionen af ​​en ret linje i rummet bestemmes fuldstændigt ved at angive et hvilket som helst af dets fikspunkter M 1 og en vektor parallel med denne linje.

En vektor parallel med en ret linje kaldes vejledende vektoren af ​​denne linje.

Så lad det lige l går gennem et punkt M 1 (x 1 , y 1 , z 1) liggende på en lige linje parallelt med vektoren.

Overvej et vilkårligt punkt M(x,y,z) på en lige linje. Det kan ses af figuren .

Vektorerne og er collineære, så der er sådan et tal t, hvad , hvor er multiplikatoren t kan tage enhver numerisk værdi afhængigt af punktets position M på en lige linje. Faktor t kaldes en parameter. Betegner radiusvektorerne for punkter M 1 og M henholdsvis gennem og , vi opnår . Denne ligning kaldes vektor lige linje ligning. Det viser, at hver parameterværdi t svarer til radiusvektoren for et punkt M liggende på en lige linje.

Vi skriver denne ligning i koordinatform. Læg mærke til det , og herfra

De resulterende ligninger kaldes parametrisk lige linje ligninger.

Ved ændring af parameter t koordinater ændres x, y og z og prik M bevæger sig i en lige linje.

KANONISKE LIGNINGER DIREKTE

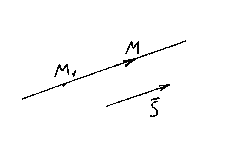
Lade M 1 (x 1 , y 1 , z 1) - et punkt, der ligger på en lige linje l, og er dens retningsvektor. Igen, tag et vilkårligt punkt på en lige linje M(x,y,z) og overvej vektoren.

Det er klart, at vektorerne og er kollineære, så deres respektive koordinater skal være proportionale, derfor

– kanonisk lige linje ligninger.

Bemærkning 1. Bemærk, at linjens kanoniske ligninger kunne opnås fra de parametriske ligninger ved at eliminere parameteren t. Faktisk ud fra de parametriske ligninger, vi får eller .

Eksempel. Skriv ligningen for en ret linje på en parametrisk måde.

Betegn , derfor x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Bemærkning 2. Lad linjen stå vinkelret på en af ​​koordinatakserne, for eksempel aksen Okse. Så er linjens retningsvektor vinkelret Okse, Følgelig, m=0. Følgelig antager de parametriske ligninger for den rette linje formen

Eliminering af parameteren fra ligningerne t, får vi ligningerne for den rette linje i formen

Men også i dette tilfælde er vi enige om formelt at skrive de kanoniske ligninger for den rette linje i formen . Så hvis nævneren for en af ​​brøkerne er nul, betyder det, at linjen er vinkelret på den tilsvarende koordinatakse.

Tilsvarende de kanoniske ligninger svarer til en ret linje vinkelret på akserne Okse og Åh eller parallel akse Oz.

Eksempler.

GENERELLE LIGNINGER EN DIREKTE LINJE SOM EN AFSNITSLINJE AF TO FLY

Gennem hver lige linje i rummet passerer et uendeligt antal planer. Hvilke som helst to af dem, der krydser hinanden, definerer det i rummet. Derfor er ligningerne for alle to sådanne planer, betragtet under ét, ligningerne for denne linje.

Generelt er to ikke-parallelle planer givet af de generelle ligninger

bestemme deres skæringslinje. Disse ligninger kaldes generelle ligninger lige.

Eksempler.

Konstruer en ret linje givet ved ligninger

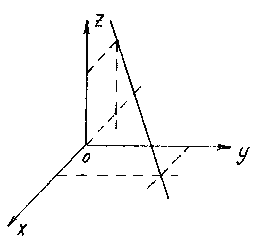
For at konstruere en linje er det nok at finde to af dens punkter. Den nemmeste måde er at vælge skæringspunkterne for linjen med koordinatplanerne. For eksempel skæringspunktet med planet xOy vi får ud fra ligningerne for en ret linje, forudsat z= 0:

Løser vi dette system, finder vi pointen M 1 (1;2;0).

Tilsvarende, forudsat y= 0, får vi skæringspunktet for linjen med planet xOz:

Fra de generelle ligninger for en ret linje kan man gå videre til dens kanoniske eller parametriske ligninger. For at gøre dette skal du finde et punkt M 1 på linjen og linjens retningsvektor.

Punktkoordinater M 1 får vi fra dette ligningssystem, hvilket giver en af ​​koordinaterne en vilkårlig værdi. For at finde retningsvektoren skal du bemærke, at denne vektor skal være vinkelret på begge normalvektorer og . Derfor for retningsvektoren for den rette linje l du kan tage krydsproduktet af normale vektorer:

.

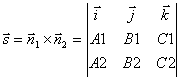Eksempel. Angiv de generelle ligninger for den rette linje til den kanoniske form.

Find et punkt på en lige linje. For at gøre dette vælger vi vilkårligt en af ​​koordinaterne, f.eks. y= 0 og løs ligningssystemet:

Normalvektorerne for de planer, der definerer linjen, har koordinater Derfor vil retningsvektoren være lige

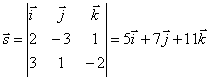. Følgelig, l: .

VINKEL MELLEM RETTIGHEDER

hjørne mellem rette linjer i rummet vil vi kalde enhver af de tilstødende vinkler dannet af to rette linjer trukket gennem et vilkårligt punkt parallelt med dataene.

Lad to rette linjer angives i rummet:

Det er klart, at vinklen φ mellem linjerne kan tages som vinklen mellem deres retningsvektorer og . Siden , så ifølge formlen for cosinus af vinklen mellem vektorerne får vi

hjørne mellem rette linjer i rummet vil vi kalde enhver af de tilstødende vinkler dannet af to rette linjer trukket gennem et vilkårligt punkt parallelt med dataene.

Lad to rette linjer angives i rummet:

Det er klart, at vinklen φ mellem linjerne kan tages som vinklen mellem deres retningsvektorer og . Siden , så ifølge formlen for cosinus af vinklen mellem vektorerne får vi

Betingelserne for parallelitet og vinkelrethed af to linjer svarer til betingelserne for parallelitet og vinkelrethed af deres retningsvektorer og:

To lige er parallelle hvis og kun hvis deres respektive koefficienter er proportionale, dvs. l 1 parallel l 2 hvis og kun hvis parallelt .

To lige vinkelret hvis og kun hvis summen af ​​produkterne af de tilsvarende koefficienter er lig med nul: .

På mål mellem linje og fly

Lad stregen d- ikke vinkelret på planet θ;
d′− projektion af en ret linje d til planet θ;
Den mindste af vinklerne mellem rette linjer d og d"Vi ringer vinkel mellem linje og plan.
Lad os betegne det som φ=( d,θ)
Hvis en d⊥θ , derefter ( d,θ)=π/2

Oi→j→k→− rektangulært koordinatsystem.
Planligning:

θ: Økse+Ved+cz+D=0

Vi mener, at linjen er givet af et punkt og en retningsvektor: d[M 0,s→]
Vektor n→(EN,B,C)⊥θ
Så er det tilbage at finde ud af vinklen mellem vektorerne n→ og s→, benævn det som γ=( n→,s→).

Hvis vinklen γ<π/2 , то искомый угол φ=π/2−γ .

Hvis vinklen γ>π/2 , så er den nødvendige vinkel φ=γ−π/2

sinφ=sin(2π−γ)=cosγ

sinφ=sin(γ−2π)=−cosγ

Derefter, vinkel mellem linje og plan kan beregnes ved hjælp af formlen:

sinφ=∣cosγ∣=∣ ∣ Ap 1+bp 2+cp 3∣ ∣ √EN 2+B 2+C 2√s 21+s 22+s 23

Spørgsmål 29. Begrebet en kvadratisk form. Fortegnsbestemtheden af ​​kvadratiske former.

Kvadratisk form j (x 1, x 2, ..., x n) n reelle variable x 1, x 2, ..., x n kaldes summen af ​​formen
, (1)

hvor aij er nogle tal kaldet koefficienter. Uden tab af almenhed kan vi antage det aij = en ji.

Den kvadratiske form kaldes gyldig, hvis aij О GR. Matrix af kvadratisk form kaldes matrixen sammensat af dens koefficienter. Kvadratisk form (1) svarer til en unik symmetrisk matrix
dvs. A T = A. Derfor kan kvadratisk form (1) skrives på matrixform j ( x) = x T Ah, hvor x T = (x 1 x 2 … x n). (2)

Og omvendt svarer enhver symmetrisk matrix (2) til en unik kvadratisk form op til notationen af ​​variable.

Rangen af ​​den kvadratiske form kaldes rangen af ​​dens matrix. Den kvadratiske form kaldes ikke-degenereret, hvis dens matrix er ikke-singular MEN. (husk på, at matrixen MEN kaldes ikke-degenereret, hvis dens determinant er ikke-nul). Ellers er den kvadratiske form degenereret.

positiv bestemt(eller strengt taget positiv) hvis

j ( x) > 0 , for enhver x = (x 1 , x 2 , …, x n), Udover x = (0, 0, …, 0).

Matrix MEN positiv bestemt andengradsform j ( x) kaldes også positiv bestemt. Derfor svarer en positiv bestemt kvadratisk form til en unik positiv bestemt matrix og omvendt.

Den kvadratiske form (1) kaldes negativ bestemt(eller strengt negativ) hvis

j ( x) < 0, для любого x = (x 1 , x 2 , …, x n), Desuden x = (0, 0, …, 0).

På samme måde som ovenfor kaldes en negativ-definit kvadratisk matrix også negativ-definit.

Derfor er en positivt (negativt) bestemt andengradsform j ( x) når minimum (maksimum) værdi j ( X*) = 0 for X* = (0, 0, …, 0).

Bemærk, at de fleste kvadratiske former ikke er tegnbestemte, det vil sige, at de hverken er positive eller negative. Sådanne kvadratiske former forsvinder ikke kun ved oprindelsen af ​​koordinatsystemet, men også på andre punkter.

Hvornår n> 2, kræves særlige kriterier for at kontrollere fortegnsbestemtheden af ​​en kvadratisk form. Lad os overveje dem.

Større mindreårige andengradsform kaldes mindreårige:

det vil sige, at der er tale om mindreårige af orden 1, 2, …, n matricer MEN, placeret i øverste venstre hjørne, falder den sidste af dem sammen med matrixens determinant MEN.

Kriterium for positiv bestemthed (Sylvester-kriterium)

x) = x T Ah er positiv bestemt, er det nødvendigt og tilstrækkeligt, at alle primære mindreårige i matrixen MEN var positive, dvs. M 1 > 0, M 2 > 0, …, M n > 0. Kriterium for negativ sikkerhed For at den andengradsform j ( x) = x T Ah er negativ bestemt, er det nødvendigt og tilstrækkeligt, at dens primære mindreårige af lige orden er positive, og de af ulige orden er negative, dvs. M 1 < 0, M 2 > 0, M 3 < 0, …, (–1)n

Dette materiale er afsat til et sådant koncept som vinklen mellem to krydsende lige linjer. I det første afsnit vil vi forklare, hvad det er og vise det i illustrationer. Derefter vil vi analysere, hvordan du kan finde sinus, cosinus for denne vinkel og selve vinklen (vi vil separat overveje tilfælde med et plan og tredimensionelt rum), vi vil give de nødvendige formler og vise med eksempler, hvordan de nøjagtigt anvendes i praksis.

Yandex.RTB R-A-339285-1

For at forstå, hvad en vinkel dannet ved skæringspunktet mellem to linjer er, skal vi huske selve definitionen af ​​en vinkel, vinkelret og et skæringspunkt.

Definition 1

Vi kalder to linjer, der skærer hinanden, hvis de har ét fælles punkt. Dette punkt kaldes skæringspunktet mellem de to linjer.

Hver linje er opdelt efter skæringspunktet i stråler. I dette tilfælde danner begge linjer 4 vinkler, hvoraf to er lodrette og to er tilstødende. Hvis vi kender målet for en af ​​dem, så kan vi bestemme de øvrige resterende.

Lad os sige, at vi ved, at en af ​​vinklerne er lig med α. I et sådant tilfælde vil den vinkel, der er lodret i forhold til den, også være lig med α. For at finde de resterende vinkler skal vi beregne forskellen 180 ° - α . Hvis α er lig med 90 grader, vil alle vinkler være rigtige. Linjer, der skærer i rette vinkler, kaldes vinkelrette (en separat artikel er afsat til begrebet vinkelrethed).

Tag et kig på billedet:

Lad os gå videre til formuleringen af ​​hoveddefinitionen.

Definition 2

Vinklen dannet af to skærende linjer er målet for den mindste af de 4 vinkler, der danner disse to linjer.

En vigtig konklusion skal drages ud fra definitionen: størrelsen af ​​vinklen i dette tilfælde vil blive udtrykt ved et hvilket som helst reelt tal i intervallet (0 , 90 ] . Hvis linjerne er vinkelrette, så vil vinklen mellem dem under alle omstændigheder være lig med 90 grader.

Evnen til at finde målet for vinklen mellem to skærende linjer er nyttig til at løse mange praktiske problemer. Løsningsmetoden kan vælges blandt flere muligheder.

Til at begynde med kan vi tage geometriske metoder. Hvis vi ved noget om yderligere vinkler, så kan vi forbinde dem med den vinkel, vi har brug for, ved at bruge egenskaberne for ens eller lignende former. Hvis vi for eksempel kender siderne i en trekant og skal beregne vinklen mellem de linjer, som disse sider er placeret på, så er cosinussætningen velegnet til at løse. Hvis vi har en retvinklet trekant i betingelsen, så skal vi til beregninger også kende vinklens sinus, cosinus og tangens.

Koordinatmetoden er også meget praktisk til at løse problemer af denne type. Lad os forklare, hvordan man bruger det korrekt.

Vi har et rektangulært (kartesisk) koordinatsystem O x y med to rette linjer. Lad os betegne dem med bogstaverne a og b. I dette tilfælde kan rette linjer beskrives ved hjælp af en hvilken som helst ligning. De oprindelige linjer har et skæringspunkt M . Hvordan bestemmer man den ønskede vinkel (lad os betegne den α) mellem disse linjer?

Lad os starte med formuleringen af ​​det grundlæggende princip om at finde en vinkel under givne forhold.

Vi ved, at sådanne begreber som retning og normalvektor er tæt forbundet med begrebet en ret linje. Hvis vi har ligningen for en ret linje, kan vi tage koordinaterne for disse vektorer fra den. Vi kan gøre dette for to skærende linjer på én gang.

Vinklen dannet af to skærende linjer kan findes ved hjælp af:

• vinkel mellem retningsvektorer;
• vinkel mellem normale vektorer;
• vinklen mellem den ene linjes normalvektor og den andens retningsvektor.

Lad os nu se på hver metode separat.

1. Antag, at vi har en linje a med retningsvektor a → = (a x , a y) og en linje b med retningsvektor b → (b x , b y) . Lad os nu afsætte to vektorer a → og b → fra skæringspunktet. Derefter vil vi se, at de bliver placeret på hver deres linje. Så har vi fire muligheder for deres relative stilling. Se illustration:

Hvis vinklen mellem to vektorer ikke er stump, så vil det være den vinkel, vi skal bruge mellem de skærende linjer a og b. Hvis den er stump, så vil den ønskede vinkel være lig med vinklen, der støder op til vinklen a → , b → ^ . Således er α = a → , b → ^ hvis a → , b → ^ ≤ 90 ° og α = 180 ° - a → , b → ^ hvis a → , b → ^ > 90 ° .

Baseret på det faktum, at cosinus af lige vinkler er ens, kan vi omskrive de resulterende ligheder som følger: cos α = cos a → , b → ^ hvis a → , b → ^ ≤ 90 ° ; cos α = cos 180 ° - a → , b → ^ = - cos a → , b → ^ hvis a → , b → ^ > 90 ° .

I det andet tilfælde blev reduktionsformler brugt. På denne måde

cos α cos a → , b → ^ , cos a → , b → ^ ≥ 0 - cos a → , b → ^ , cos a → , b → ^< 0 ⇔ cos α = cos a → , b → ^

Lad os skrive den sidste formel med ord:

Definition 3

Cosinus for vinklen dannet af to skærende linjer vil være lig med modulet af cosinus af vinklen mellem dens retningsvektorer.

Den generelle form for formlen for cosinus af vinklen mellem to vektorer a → = (a x, a y) og b → = (b x, b y) ser sådan ud:

cos a → , b → ^ = a → , b → ^ a → b → = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2

Ud fra det kan vi udlede formlen for cosinus af vinklen mellem to givne linjer:

cos α = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2 = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2

Så kan selve vinklen findes ved hjælp af følgende formel:

α = a r c cos a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2

Her er a → = (a x , a y) og b → = (b x , b y) retningsvektorerne for de givne linjer.

Lad os give et eksempel på løsning af problemet.

Eksempel 1

I et rektangulært koordinatsystem er to skærende linjer a og b givet på planet. De kan beskrives med parametriske ligninger x = 1 + 4 · λ y = 2 + λ λ ∈ R og x 5 = y - 6 - 3 . Beregn vinklen mellem disse linjer.

Løsning

Vi har en parametrisk ligning i betingelsen, hvilket betyder, at vi for denne rette linje straks kan nedskrive koordinaterne for dens retningsvektor. For at gøre dette skal vi tage værdierne af koefficienterne ved parameteren, dvs. linjen x = 1 + 4 λ y = 2 + λ λ ∈ R vil have en retningsvektor a → = (4 , 1) .

Den anden rette linje er beskrevet ved hjælp af den kanoniske ligning x 5 = y - 6 - 3 . Her kan vi tage koordinaterne fra nævnerne. Denne linje har således en retningsvektor b → = (5 , - 3) .

Dernæst går vi direkte videre til at finde vinklen. For at gøre dette skal du blot erstatte de tilgængelige koordinater for de to vektorer i ovenstående formel α = a r c cos a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2 . Vi får følgende:

α = a r c cos 4 5 + 1 (- 3) 4 2 + 1 2 5 2 + (- 3) 2 = a r c cos 17 17 34 = a r c cos 1 2 = 45°

Svar: Disse linjer danner en vinkel på 45 grader.

Vi kan løse et lignende problem ved at finde vinklen mellem normale vektorer. Hvis vi har en linje a med en normalvektor n a → = (n a x , n a y) og en linje b med en normalvektor n b → = (n b x , n b y) , så vil vinklen mellem dem være lig med vinklen mellem n a → og n b → eller den vinkel, der støder op til n a → , n b → ^ . Denne metode er vist på billedet:

Formlerne til beregning af cosinus af vinklen mellem skærende linjer og denne vinkel selv ved hjælp af koordinaterne for normale vektorer ser sådan ud:

cos α = cos n a → , n b → ^ = n a x n b x + n a y + n b y n a x 2 + n a y 2 n b x 2 + n b y 2

Her betegner n a → og n b → normalvektorerne for to givne linjer.

Eksempel 2

To rette linjer er givet i et rektangulært koordinatsystem ved hjælp af ligningerne 3 x + 5 y - 30 = 0 og x + 4 y - 17 = 0 . Find sinus, cosinus af vinklen mellem dem, og størrelsen af ​​denne vinkel selv.

Løsning

De oprindelige rette linjer er givet ved hjælp af normale lige linjeligninger på formen A x + B y + C = 0 . Betegn normalvektoren n → = (A , B) . Lad os finde koordinaterne for den første normalvektor for en ret linje og skrive dem ned: n a → = (3 , 5) . For den anden linje x + 4 y - 17 = 0 vil normalvektoren have koordinater n b → = (1 , 4) . Tilføj nu de opnåede værdier til formlen og beregn totalen:

cos α = cos n a → , n b → ^ = 3 1 + 5 4 3 2 + 5 2 1 2 + 4 2 = 23 34 17 = 23 2 34

Hvis vi kender cosinus af en vinkel, så kan vi beregne dens sinus ved hjælp af den grundlæggende trigonometriske identitet. Da vinklen α dannet af rette linjer ikke er stump, så sin α \u003d 1 - cos 2 α \u003d 1 - 23 2 34 2 \u003d 7 2 34.

I dette tilfælde er α = a r c cos 23 2 34 = a r c sin 7 2 34 .

Svar: cos α = 23 2 34 , sin α = 7 2 34 , α = a r c cos 23 2 34 = a r c sin 7 2 34

Lad os analysere det sidste tilfælde - at finde vinklen mellem linjerne, hvis vi kender koordinaterne for retningsvektoren for en linje og normalvektoren for den anden.

Antag, at linje a har en retningsvektor a → = (a x , a y) , og linje b har en normalvektor n b → = (n b x , n b y) . Vi er nødt til at udskyde disse vektorer fra skæringspunktet og overveje alle muligheder for deres relative position. Se billede:

Hvis vinklen mellem de givne vektorer ikke er mere end 90 grader, viser det sig, at den vil komplementere vinklen mellem a og b til en ret vinkel.

a → , n b → ^ = 90 ° - α hvis a → , n b → ^ ≤ 90 ° .

Hvis det er mindre end 90 grader, får vi følgende:

a → , n b → ^ > 90 ° , derefter a → , n b → ^ = 90 ° + α

Ved at bruge reglen om lighed af cosinus af lige vinkler skriver vi:

cos a → , n b → ^ = cos (90 ° - α) = sin α for a → , n b → ^ ≤ 90 ° .

cos a → , n b → ^ = cos 90 ° + α = - sin α ved a → , n b → ^ > 90 ° .

På denne måde

sin α = cos a → , n b → ^ , a → , n b → ^ ≤ 90 ° - cos a → , n b → ^ , a → , n b → ^ > 90 ° ⇔ sin α = cos a → , n b → ^ , a → , n b → ^ > 0 - cos a → , n b → ^ , a → , n b → ^< 0 ⇔ ⇔ sin α = cos a → , n b → ^

Lad os formulere en konklusion.

Definition 4

For at finde sinus af vinklen mellem to linjer, der skærer hinanden i et plan, skal du beregne modulet for cosinus af vinklen mellem retningsvektoren for den første linje og normalvektoren for den anden.

Lad os skrive de nødvendige formler ned. Find sinus af en vinkel:

sin α = cos a → , n b → ^ = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2

Find selve hjørnet:

α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2

Her er a → retningsvektoren for den første linje, og n b → er normalvektoren for den anden.

Eksempel 3

To skærende linjer er givet ved ligningerne x - 5 = y - 6 3 og x + 4 y - 17 = 0 . Find skæringsvinklen.

Løsning

Vi tager koordinaterne for retnings- og normalvektoren fra de givne ligninger. Det viser sig a → = (- 5 , 3) ​​og n → b = (1 , 4) . Vi tager formlen α \u003d a r c sin \u003d a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2 og overvejer:

α = a r c sin = - 5 1 + 3 4 (- 5) 2 + 3 2 1 2 + 4 2 = a r c sin 7 2 34

Bemærk, at vi tog ligningerne fra den forrige opgave og fik nøjagtig det samme resultat, men på en anden måde.

Svar:α = a r c sin 7 2 34

Her er en anden måde at finde den ønskede vinkel ved hjælp af hældningskoefficienterne for givne linjer.

Vi har en linje a , som er defineret i et rektangulært koordinatsystem ved hjælp af ligningen y = k 1 · x + b 1 , og en linje b , defineret som y = k 2 · x + b 2 . Disse er ligninger af linjer med en hældning. For at finde skæringsvinklen skal du bruge formlen:

α = a r c cos k 1 k 2 + 1 k 1 2 + 1 k 2 2 + 1, hvor k 1 og k 2 er hældningerne af de givne linjer. For at opnå denne registrering blev formler til bestemmelse af vinklen gennem koordinaterne af normale vektorer brugt.

Eksempel 4

Der er to rette linjer, der skærer hinanden i planet, givet ved ligningerne y = - 3 5 x + 6 og y = - 1 4 x + 17 4 . Beregn skæringsvinklen.

Løsning

Hældningerne på vores linjer er lig med k 1 = - 3 5 og k 2 = - 1 4 . Lad os tilføje dem til formlen α = a r c cos k 1 k 2 + 1 k 1 2 + 1 k 2 2 + 1 og beregne:

α = a r c cos - 3 5 - 1 4 + 1 - 3 5 2 + 1 - 1 4 2 + 1 = a r c cos 23 20 34 24 17 16 = a r c cos 23 2 34

Svar:α = a r c cos 23 2 34

I konklusionerne af dette afsnit skal det bemærkes, at formlerne til at finde vinklen, der er givet her, ikke skal læres udenad. For at gøre dette er det nok at kende koordinaterne for guiderne og/eller normalvektorerne for de givne linjer og være i stand til at bestemme dem ved hjælp af forskellige typer ligninger. Men formlerne til beregning af cosinus af en vinkel er bedre at huske eller skrive ned.

Hvordan man beregner vinklen mellem skærende linjer i rummet

Beregningen af ​​en sådan vinkel kan reduceres til beregningen af ​​retningsvektorernes koordinater og bestemmelsen af ​​størrelsen af ​​vinklen dannet af disse vektorer. Til sådanne eksempler bruger vi den samme begrundelse, som vi har givet før.

Lad os sige, at vi har et rektangulært koordinatsystem placeret i 3D-rummet. Den indeholder to linjer a og b med skæringspunktet M . For at beregne koordinaterne for retningsvektorerne skal vi kende ligningerne for disse linjer. Betegn retningsvektorerne a → = (a x , a y , a z) og b → = (b x , b y , b z) . For at beregne cosinus af vinklen mellem dem bruger vi formlen:

cos α = cos a → , b → ^ = a → , b → a → b → = a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2

For at finde selve vinklen har vi brug for denne formel:

α = a r c cos a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2

Eksempel 5

Vi har en ret linje defineret i 3D-rum ved hjælp af ligningen x 1 = y - 3 = z + 3 - 2 . Det er kendt, at det skærer Oz-aksen. Beregn skæringsvinklen og cosinus for denne vinkel.

Løsning

Lad os betegne den vinkel, der skal beregnes, med bogstavet α. Lad os nedskrive koordinaterne for retningsvektoren for den første rette linje - a → = (1 , - 3 , - 2) . For den anvendte akse kan vi tage koordinatvektoren k → = (0 , 0 , 1) som en guide. Vi har modtaget de nødvendige data og kan tilføje dem til den ønskede formel:

cos α = cos a → , k → ^ = a → , k → a → k → = 1 0 - 3 0 - 2 1 1 2 + (- 3) 2 + (- 2) 2 0 2 + 0 2 + 1 2 = 2 8 = 1 2

Som et resultat fik vi, at den vinkel, vi har brug for, vil være lig med a r c cos 1 2 = 45 °.

Svar: cos α = 1 2 , α = 45 ° .

Hvis du bemærker en fejl i teksten, skal du markere den og trykke på Ctrl+Enter

Lad linjer gives i rummet l og m. Gennem et punkt A i rummet tegner vi lige linjer l 1 || l og m 1 || m(Fig. 138).

Bemærk at punktet A kan vælges vilkårligt, især kan det ligge på en af ​​de givne linjer. Hvis lige l og m skærer hinanden, så kan A tages som skæringspunktet for disse linjer ( l 1 =l og m 1 = m).

Vinkel mellem ikke-parallelle linjer l og m er værdien af ​​den mindste af de tilstødende vinkler dannet af skærende rette linjer l 1 og m 1 (l 1 || l, m 1 || m). Vinklen mellem parallelle linjer antages at være nul.

Vinkel mellem linjer l og m angivet med \(\widehat((l;m)) \). Af definitionen følger, at hvis det måles i grader, så 0 ° < \(\widehat((l;m)) \) < 90°, og hvis i radianer, så 0 < \(\widehat((l;m)) \) < π / 2 .

En opgave. Terningen ABCDA 1 B 1 C 1 D 1 er givet (fig. 139).

Find vinklen mellem rette linjer AB og DC 1 .

Lige AB og DC 1 krydsning. Da linjen DC er parallel med linjen AB, er vinklen mellem linjerne AB og DC 1 ifølge definitionen lig med \(\widehat(C_(1)DC)\).

Derfor \(\widehat((AB;DC_1))\) = 45°.

Direkte l og m hedder vinkelret, hvis \(\widehat((l;m)) \) = π / 2. For eksempel i en terning

Beregning af vinklen mellem linjer.

Problemet med at beregne vinklen mellem to rette linjer i rummet løses på samme måde som i planet. Betegn med φ vinklen mellem linjerne l 1 og l 2 , og gennem ψ - vinklen mellem retningsvektorerne -en og b disse lige linjer.

Så hvis

ψ <90° (рис. 206, а), то φ = ψ; если же ψ >90° (fig. 206.6), så φ = 180° - ψ. Det er indlysende, at i begge tilfælde er ligheden cos φ = |cos ψ| sand. Ifølge formlen (cosinus af vinklen mellem ikke-nul vektorer a og b er lig med skalarproduktet af disse vektorer divideret med produktet af deres længder) har vi

$$ cos\psi = cos\widehat((a; b)) = \frac(a\cdot b)(|a|\cdot |b|) $$

Følgelig,

$$ cos\phi = \frac(|a\cdot b|)(|a|\cdot |b|) $$

Lad linjerne være givet ved deres kanoniske ligninger

$$ \frac(x-x_1)(a_1)=\frac(y-y_1)(a_2)=\frac(z-z_1)(a_3) \;\; og \;\; \frac(x-x_2)(b_1)=\frac(y-y_2)(b_2)=\frac(z-z_2)(b_3) $$

Derefter bestemmes vinklen φ mellem linjerne ved hjælp af formlen

$$ cos\phi = \frac(|a_(1)b_1+a_(2)b_2+a_(3)b_3|)(\sqrt((a_1)^2+(a_2)^2+(a_3)^2 )\sqrt((b_1)^2+(b_2)^2+(b_3)^2)) (1)$$

Hvis en af ​​linjerne (eller begge) er givet ved ikke-kanoniske ligninger, skal du for at beregne vinklen finde koordinaterne for retningsvektorerne for disse linjer og derefter bruge formel (1).

Opgave 1. Beregn vinkel mellem linjer

$$ \frac(x+3)(-\sqrt2)=\frac(y)(\sqrt2)=\frac(z-7)(-2) \;\;og\;\; \frac(x)(\sqrt3)=\frac(y+1)(\sqrt3)=\frac(z-1)(\sqrt6) $$

Retningsvektorer af rette linjer har koordinater:

a \u003d (-√2; √2; -2), b = (√3 ; √3 ; √6 ).

Ved formel (1) finder vi

$$ cos\phi = \frac(|-\sqrt6+\sqrt6-2\sqrt6|)(\sqrt(2+2+4)\sqrt(3+3+6))=\frac(2\sqrt6)( 2\sqrt2\cdot 2\sqrt3)=\frac(1)(2) $$

Derfor er vinklen mellem disse linjer 60°.

Opgave 2. Beregn vinkel mellem linjer

$$ \begin(cases)3x-12z+7=0\\x+y-3z-1=0\end(cases) og \begin(cases)4x-y+z=0\\y+z+1 =0\end(cases) $$

Bag guidevektoren -en den første rette linje tager vi vektorproduktet af normale vektorer n 1 = (3; 0; -12) og n 2 = (1; 1; -3) planer, der definerer denne linje. Ved formlen \(=\begin(vmatrix) i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end(vmatrix) \) får vi

$$ a==\begin(vmatrix) i & j & k \\ 3 & 0 & -12 \\ 1 & 1 & -3 \end(vmatrix)=12i-3i+3k $$

På samme måde finder vi retningsvektoren for den anden rette linje:

$$ b=\begin(vmatrix) i & j & k \\ 4 & -1 & 1 \\ 0 & 1 & 1 \end(vmatrix)=-2i-4i+4k $$

Men formel (1) beregner cosinus for den ønskede vinkel:

$$ cos\phi = \frac(|12\cdot (-2)-3(-4)+3\cdot 4|)(\sqrt(12^2+3^2+3^2)\sqrt(2) ^2+4^2+4^2))=0 $$

Derfor er vinklen mellem disse linjer 90°.

Opgave 3. I den trekantede pyramide MAVS er kanterne MA, MB og MC indbyrdes vinkelrette, (fig. 207);

deres længder er henholdsvis lig med 4, 3, 6. Punkt D er den midterste [MA]. Find vinklen φ mellem linjerne CA og DB.

Lad SA og DB være retningsvektorerne for linjerne SA og DB.

Lad os tage punktet M som udgangspunktet for koordinaterne. Ved opgavebetingelsen har vi A (4; 0; 0), B(0; 0; 3), C(0; 6; 0), D (2; 0; 0). Derfor \(\overhøjrepil(CA)\) = (4; - 6;0), \(\overhøjrepil(DB)\)= (-2; 0; 3). Vi bruger formel (1):

$$ cos\phi=\frac(|4\cdot (-2)+(-6)\cdot 0+0\cdot 3|)(\sqrt(16+36+0)\sqrt(4+0+9 )) $$

Ifølge cosinustabellen finder vi, at vinklen mellem de rette linjer CA og DB er ca. 72°.

Hvis to vilkårlige punkter M 1 (x 1, y 1, z 1) og M 2 (x 2, y 2, z 2) er markeret på en ret linje i rummet, så skal koordinaterne for disse punkter opfylde ligningen for lige linje opnået ovenfor:

Derudover kan vi for punkt M 1 skrive:

.

Løser vi disse ligninger sammen får vi:

.

Dette er ligningen for en ret linje, der går gennem to punkter i rummet.

Generelle ligninger for en ret linje i rummet.

Ligningen for en ret linje kan betragtes som ligningen for en skæringslinje mellem to planer.

Generelle ligninger for en ret linje i koordinatform:

Et praktisk problem består ofte i at bringe linjeligningerne i generel form til den kanoniske form.

For at gøre dette skal du finde et vilkårligt punkt på linjen og tallene m, n, s.

I dette tilfælde kan retningsvektoren for en ret linje findes som et vektorprodukt af normalvektorerne til de givne planer.

Eksempel. Find den kanoniske ligning, hvis den rette linje er givet i formen:

For at finde et vilkårligt punkt på en ret linje, lad os tage dets koordinat x = 0, og derefter erstatte denne værdi i det givne ligningssystem.

De der. A(0, 2, 1).

Vi finder komponenterne i den rette linjes retningsvektor.

Så linjens kanoniske ligninger:

Eksempel. Bring til den kanoniske form ligningen for en ret linje, givet i formen:

For at finde et vilkårligt punkt på den rette linje, som er skæringslinjen mellem ovenstående planer, tager vi z = 0. Så:

;

2x - 9x - 7 = 0;

Vi får: A(-1; 3; 0).

Retningsvektor direkte: .

Vinkel mellem fly.

Vinklen mellem to planer i rummet  er relateret til vinklen mellem normalerne til disse planer  1 ved relationen:  =  1 eller  = 180 0 -  1, dvs.

cos = cos 1 .

Lad os definere vinklen  1 . Det er kendt, at planer kan defineres ved relationerne:

, hvor

(Ai, B1, C1), (A2, B2, C2). Vi finder vinklen mellem normalvektorerne ud fra deres skalarprodukt:

.

Således findes vinklen mellem planerne ved formlen:

Valget af tegnet for cosinus afhænger af hvilken vinkel mellem planerne der skal findes - spids eller stump ved siden af.

Betingelser for parallelitet og vinkelrethed af planer.

Ud fra ovenstående formel til at finde vinklen mellem planerne kan man finde betingelserne for planernes parallelitet og vinkelrethed.

For at planerne skal være vinkelrette, er det nødvendigt og tilstrækkeligt, at cosinus for vinklen mellem planerne er lig nul. Denne betingelse er opfyldt, hvis:

Planerne er parallelle, normalvektorerne er kollineære:  . Denne betingelse er opfyldt, hvis: .

Vinkel mellem linjer i rummet.

Lad to rette linjer gives i rummet. Deres parametriske ligninger er:

Vinklen mellem linjerne  og vinklen mellem retningsvektorerne  af disse linjer er relateret af relationen:  =  1 eller  = 180 0 -  1 . Vinklen mellem retningsvektorerne findes ud fra skalarproduktet. På denne måde:

.

Betingelser for parallelitet og vinkelrethed af linjer i rummet.

For at to linjer kan være parallelle, er det nødvendigt og tilstrækkeligt, at disse linjers retningsvektorer er kollineære, dvs. deres respektive koordinater var proportionale.